Frequentist vs. Bayesian statistics for A/B testing

As product management continues to evolve, data-driven decision-making is becoming a more reliable approach as it provides direction and creates an efficient way of working. The growing reliance on data has led to the development of intricate mechanisms for data retrieval and analysis. Over time, the mechanisms for drawing conclusions from this data have also advanced significantly.

One widely used methodology for determining the optimal output between two alternatives is A/B testing, sometimes also known as split testing. This article delves into the two predominant statistical frameworks utilized in product A/B testing: Bayesian and frequentist methods. By the end, you should feel confident selecting a method and implementing A/B testing with your product.

Introduction to the frequentist vs. Bayesian approach to A/B testing

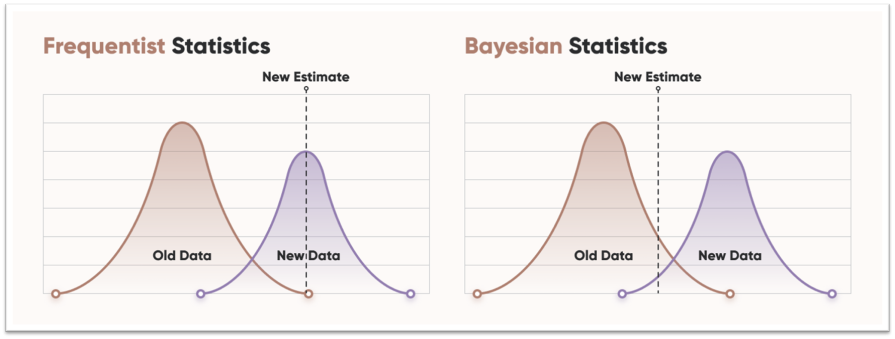
Frequentist statistics emphasizes objective data analysis. It minimizes the influence of prior biases to derive conclusions strictly from observed probabilities.

For instance, when assessing a driving route based on historical traffic conditions, if you have experienced congestion on a specific roadway during your last three commutes, a frequentist approach would lead you to infer that this route consistently yields traffic. Based on this assessment, you either seek an alternative route or adjust your expectations and commute time.

The Bayesian approach offers a subjective framework for data analysis by integrating prior beliefs and hypotheses into the inferential process. This method emphasizes continuously updating prior assumptions based on incoming data and evolving conditions.

For instance, with a Bayesian perspective, one could incorporate additional contextual parameters such as the time of day into the analysis. During office hours, the prior assumption might lean towards expecting road congestion. However, if the analysis is conducted late in the evening, the revised assumption would involve a lower probability of congestion due to reduced traffic volume, thus informing more efficient route choices in real time.

Both statistical paradigms have distinct advantages depending on your product’s specific requirements. In contexts necessitating high-stakes decision-making devoid of prior information, the frequentist framework is preferable because it looks at situations objectively based on observable information. Conversely, a Bayesian approach is more suitable for scenarios emphasizing continuous improvement and the mitigation of cognitive biases, as it uses adaptive modeling and iterative refinement in response to evolving data landscapes.

Overview of frequentist statistics

Frequentist statistics primarily emphasizes data analysis based on the frequency or proportion of observations. For successful application and understanding of this statistical approach, it’s essential to understand these key concepts:

1. P-values — A p-value is a unit that helps you understand how likely it is to get results like the ones you observed. When you analyze data, a low P-value means that the results are unlikely to be true if the null hypothesis is correct. This indication from the P- value might lead you to reject the original idea and support a different idea called the alternative hypothesis or suggest further iteration
2. Confidence intervals — These represent a range of values (intervals) within which the valid parameter is expected to fall for a certain confidence level. For example, your result must fall between a certain pre-decided confidence level for an alternative to be concluded as a desired outcome. If the results are anything lower than the predetermined confidence level then the proposed change needs further iteration
3. Hypothesis testing — This process starts with creating two statements: the null hypothesis (H0) and the alternative hypothesis (H1). The null hypothesis suggests that there is no effect or difference. In simple terms, it means that you would keep the existing design as option one. An alternative hypothesis proposes that there is an effect or a difference, which creates a second option for you to consider

Overview of Bayesian statistics

Bayesian statistics is a way to make assumptions about changes using both previous knowledge and new data. It helps improve your understanding of what your model parameters should be based on. The following are the key concepts for executing Bayesian Statistics successfully:

1. Prior distributions — These distributions encapsulate an analyst’s beliefs or knowledge about a parameter before any data is observed. They serve as the foundational input in the Bayesian updating process
2. Posterior distributions — After the observed data is incorporated, the posterior distribution emerges as the new probability distribution that reflects updated beliefs about the parameter. This distribution is derived by applying Bayes’ theorem
3. Bayes’ theorem — Central to Bayesian inference, Bayes’ theorem quantitatively describes how to update the probability of a hypothesis (or parameter) given new evidence. It mathematically codifies the relationship between prior information and likelihoods, yielding a coherent mechanism for inference as additional data is acquired

Key differences between frequentist and Bayesian approaches

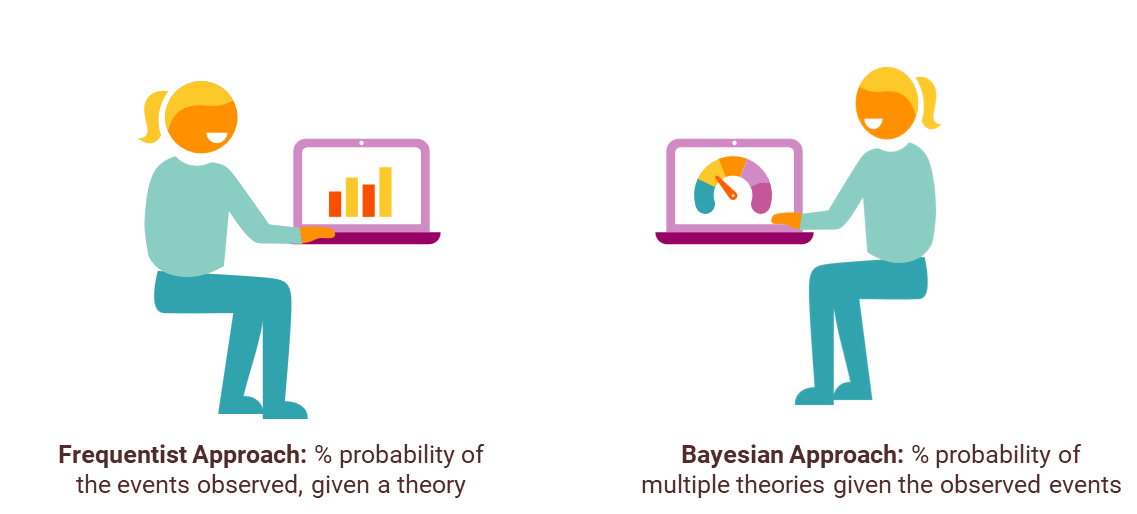
There are three main differences between these two approaches: the interpretation of probabilities, methodologies to reach to a conclusion, and inclusion of prior information.

Applications in A/B testing

Instead of investing time and money in ideas that may not appeal to users, test your ideas with user feedback and prototypes. This way, you can find effective solutions before making bigger commitments. However, some situations may favor one method over another, and each method has its limitations. Therefore, choose your approach based on a clear understanding of the basic principles, benefits, and drawbacks.

Frequentist A/B testing uses a method where researchers set up a null hypothesis and an alternative hypothesis before starting an experiment. You then conduct tests until you reach a chosen significance level, usually p < 0.05. Once this threshold is met, you make decisions based on the results. This method comes from classical statistics and focuses on how estimators and tests perform over the long run.

Bayesian A/B testing uses a flexible method that updates the chances of one version performing better than another as new data comes in. This approach helps make better decisions, especially in fast-changing situations. By using prior information and improving it based on what you observe, Bayesian methods give a clear view of how different versions perform over time.

---

Over 200k developers and product managers use LogRocket to create better digital experiences

Learn more →

---

Choosing the right approach for product decisions

When implementing A/B testing, consider these guidelines to formulate an effective testing strategy that maximizes outcomes:

1. Define clear hypotheses — Establish specific, testable hypotheses related to the user experience and expected outcomes
2. Segment your audience — Tailor your testing segments based on user demographics, behavior, or prior interactions to ensure data relevance and clarity
3. Analyze for statistical significance — Employ appropriate statistical methods to validate the results, ensuring the findings are robust and actionable

Once you have defined and analyzed the scope, consider the following implication:

1. Sample size — Frequentist methods typically require larger sample sizes to achieve reliable results, while Bayesian methods can work well with smaller samples if appropriate priors are used
2. Prior knowledge — When substantial prior knowledge or historical data is available, Bayesian methods offer a clear advantage. The frequentist approach is beneficial when starting something new without previous experience or knowledge
3. Decision-making context — Bayesian approaches provide more flexibility for quick, iterative experiments, while frequentist methods, due to their straightforward nature, are preferable for one-off, high-stakes decisions

Case studies

To help you better understand which approach to take, this section outlines a case study for each method.

Frequentist method: Team A

Team A wants to optimize their landing page to enhance conversion rates. Following several ideation sessions, the team develops a new design concept. Applying a frequentist framework, they then initiate an A/B test to compare the performance metrics of the existing landing page against those of the new design.

To attain sufficient statistical data for their analysis, the team implements the test with a sizable sample size over an extended duration, typically one month or longer. This timeframe ensures the robust data collection required to support a confident evaluation of the new landing page’s efficacy.

After analyzing the gathered data, Team A validates or refutes their hypothesis, proceeds with further enhancements based on the findings, and subsequently implements the new design across the entire user base.

Bayesian method: Team B

Team B opts to implement a Bayesian A/B testing framework, leveraging their accumulated insights from prior experiments on the landing page. During the design phase, they iteratively refine the new layout based on existing knowledge, formulating several hypotheses to assess performance.

With established baseline ideas, Team B swiftly pinpoints the optimal variant, validates their assumptions, and reaches informed decisions more rapidly regarding the superior design choice. This approach not only accelerates the testing process but also enhances the robustness of their conclusions through the integration of prior data.

Based on the new result, Team B also updates their knowledge and opinions from previous experimentation. Knowing how to analyze the data objectively when using the Bayesian method is crucial since the team can often analyze the data to confirm biases instead of updating their hypothesis.

Outcomes and lessons learned

The frequentist and Bayesian approaches present distinct advantages and drawbacks but frequently yield comparable outcomes. The crux of effective decision-making lies in adopting a data-driven methodology and leveraging feedback for iterative enhancements.

The frequentist approach facilitated straightforward, conclusive decisions but demanded considerable time and resource investment.

The Bayesian approach allows for rapid, iterative testing cycles, granting a competitive advantage in rapidly changing market environments.

Final thoughts

The choice between the frequentist and Bayesian statistical approaches in A/B testing isn’t merely a matter of preference but a strategic decision shaped by the product context, available data, and business objectives. Frequentist methods, with their long-standing prevalence and objective nature, are ideal for high-stakes, single-shot experiments where prior knowledge is minimal and results need to be clear-cut. On the other hand, Bayesian methods provide a dynamic and flexible framework, excelling in scenarios with iterative decision-making and adaptive learning.

Developing expertise in both statistical frameworks allows you to design data-driven experiments tailored to each situation’s unique requirements. Whether you want to optimize conversion rates, introduce new features, or enhance user experiences, selecting the appropriate statistical method enables impactful decisions.

Featured image source: IconScout

LogRocket generates product insights that lead to meaningful action

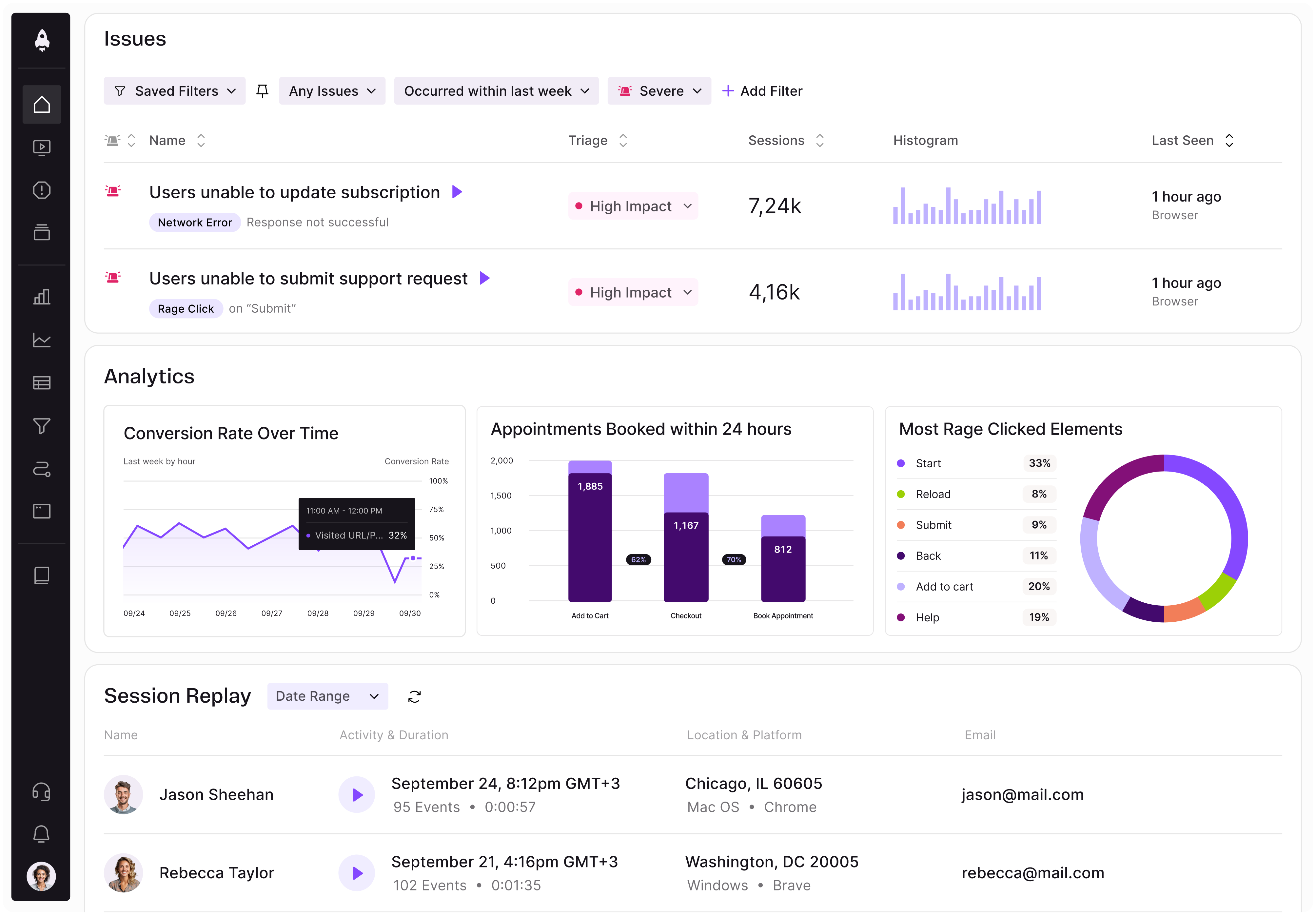
LogRocket identifies friction points in the user experience so you can make informed decisions about product and design changes that must happen to hit your goals.

With LogRocket, you can understand the scope of the issues affecting your product and prioritize the changes that need to be made. LogRocket simplifies workflows by allowing Engineering, Product, UX, and Design teams to work from the same data as you, eliminating any confusion about what needs to be done.

Get your teams on the same page — try LogRocket today.