Choosing the best JavaScript sorting algorithm for your project

Data sorting has many practical applications in modern applications, such as organizing a list of names, searching for a specific item in a database, or optimizing the performance of web applications.

There are many popular sorting algorithms, each with its advantages and disadvantages. Different data-sorting techniques can affect the speed and efficiency of computations. Inefficient sorting can result in sluggish system performance and negatively impact UX.

It’s crucial to choose the appropriate sorting technique for your needs when working with algorithms and data structures in software development. Your choice of algorithm depends on factors such as the size of the dataset and the level of sorting efficiency you desire.

In this article, we’ll discuss various sorting techniques and how to use them effectively in JavaScript projects. We’ll cover:

• Overview of JavaScript sorting algorithms
  • Insertion sort
  • Quicksort
  • Merge sort
  • Other relevant sorting algorithms
• Sorting algorithms in frontend vs. backend systems
  • Sorting in frontend systems
  • Sorting in backend systems
• Factors to consider when choosing a sorting technique
  • Data size
  • Nature of the data
  • Memory and space constraints
• Comparison table for sorting algorithms

By the end of this article, you should have a better understanding of how to choose the right sorting technique for your next project.

Overview of JavaScript sorting algorithms

You can implement popular sorting algorithms with JavaScript. Understanding these algorithms and their practical applications is essential for making informed choices when dealing with different datasets.

Insertion sort

Insertion sort is a simple sorting algorithm that repeatedly builds a sorted part of the array while iterating through the unsorted data. Insertion sort algorithms insert each unsorted element into its correct position with the sorted data:

// This function sorts an array using the Insertion Sort algorithm.
function insertionSort(arr) {
  // Start iterating from the second element of the array.
  for (let i = 1; i < arr.length; i++) {
    // 'current' is the element to be inserted in its correct place.
    let current = arr[i];

    // 'j' will help us traverse backwards from the 'i'th position.
    let j = i - 1;

    // Keep moving elements of arr[0..i-1] that are greater than 'current' 
    // one position ahead of their current position. 
    // The loop continues until we find the right spot for 'current' or reach the beginning of the array.
    while (j >= 0 && arr[j] > current) {
      arr[j + 1] = arr[j];  // Move the element one position up.
      j--;  // Move one position back in the array.
    }

    // Place 'current' in its correct position so that the elements before it are less than 'current'.
    arr[j + 1] = current;
  }

  // Return the sorted array.
  return arr;
}

const unsortedArray = [12, 11, 13, 5, 6];
const sortedArray = insertionSort(unsortedArray);

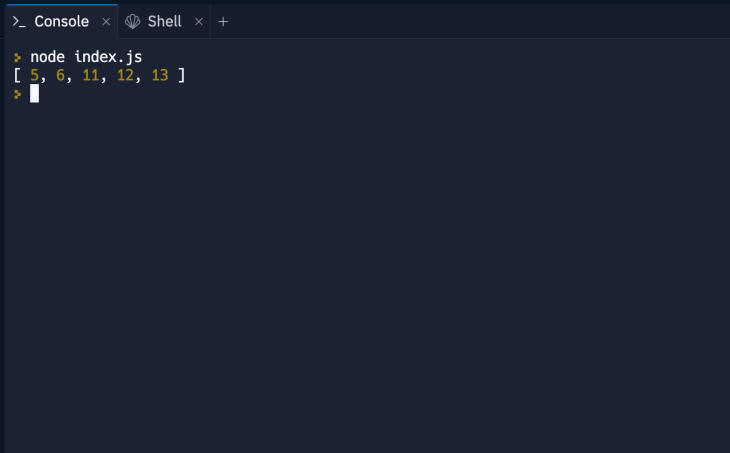
console.log(sortedArray); // This will print the sorted array.

The insertionSort function takes in an array, sorts it, and returns the sorted array. The function uses a for loop to iterate over elements and a while loop for comparison while sorting and inserting the sorted data into the array.

Here are the best-, average-, and worst-case scenarios for using the insertion sort algorithm. These scenarios describe the time complexity of the insertion sort method under different conditions in terms of the amount of computational work and memory needed:

• Best case: O(n) when the array is nearly sorted; the insertionSort function only needs to make one pass through the array
• Average case: O(n^2), where n is the number of elements; the insertionSort function may need to pass through the array multiple times
• Worst case: O(n^2) when the array is sorted in reverse order; the insertionSort function will need to do the maximum amount of work, making multiple passes through the array

Insertion sort is suitable for small datasets where elements are continuously added to a sorted list. This sorting technique is handy where the input size is small and mostly sorted already — for example, sorting a hand of playing cards:

Quicksort

The quicksort algorithm is a divide-and-conquer sorting algorithm that selects a pivot element and partitions other elements into two sub-arrays according to the size of the pivot:

function quickSort(arr) {
  // Base case: If the array has one or no elements, it is already sorted.
  if (arr.length <= 1) return arr;

  // Choosing the first element in the array as the pivot.
  const pivot = arr[0];
  // Creating two empty arrays to store elements less than (left) and greater than (right) the pivot.
  const left = [];
  const right = [];

  // Looping through the array, starting from the second element because the first is the pivot.
  for (let i = 1; i < arr.length; i++) {
    // If the current element is smaller than the pivot, push it to the 'left' array.
    if (arr[i] < pivot) left.push(arr[i]);
    // If the current element is greater than or equal to the pivot, push it to the 'right' array.
    else right.push(arr[i]);
  }

  // Concatenate the result of recursively sorting the 'left' array, the pivot, and then the 'right' array.
  // Spread syntax '...' is used to concatenate arrays.
  return [...quickSort(left), pivot, ...quickSort(right)];
}

const unsortedArray = [34, 7, 23, 32, 5, 62, 9];
const sortedArray = quickSort(unsortedArray);

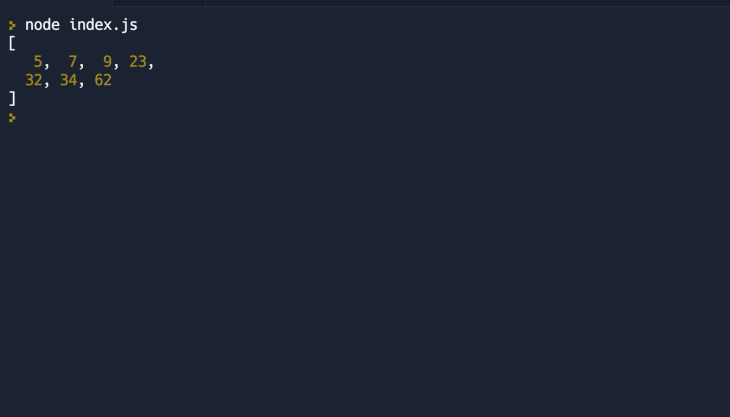
console.log(sortedArray);  // This will output: [5, 7, 9, 23, 32, 34, 62]

The quickSort function sorts an array by comparing the elements with the pivot in a for loop before returning the sorted array. The function uses two arrays for the sorting operation.

Here’s the result of calling the function with an array:

You can use quicksort in many ways, from sorting large datasets in databases to implementing sorting functions in programming languages. Similar to what we did before for the insertion sort method, let’s discuss the average and worst-case scenarios for using the quicksort algorithm:

• Average case: O(n log n) where n is the number of elements; the array is divided into a balanced manner in most of the steps, leading to a highly efficient sorting time
• Worst case: O(n^2) where the pivot element is the smallest or largest element, which leads to unbalanced partitions

Quicksort is widely used due to its average-case efficiency. It’s handy for general-purpose sorting and is often the default sorting algorithm for developers looking to sort data in an application.

Merge sort

Merge sort is another divide-and-conquer sorting algorithm that divides the unsorted list into n sublists. Each list contains one element and repeatedly merges sublists to produce new sorted sublists until only one remains:

// This function performs the merge sort algorithm on an input array.
function mergeSort(arr) {
  // If the array has one or fewer elements, it's already sorted, so we return it.
  if (arr.length <= 1) return arr;

  // Calculate the middle index of the array.
  const middle = Math.floor(arr.length / 2);

  // Split the array into two halves: left and right.
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);

  // Recursively merge, sort the left and right halves, and return the result.
  return merge(mergeSort(left), mergeSort(right));
}

// This function merges two sorted arrays into a single sorted array.

function merge(left, right) {
  // Initialize an empty result array and indices for left and right arrays.
  let result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  // Compare elements from both arrays and add the smaller element to the result.
  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] < right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // Concatenate the remaining elements from both arrays (if any) to the result.
  return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}

const unsortedArray = [34, 7, 23, 32, 5, 62, 9, 12, 3, 8];
const sortedArray = mergeSort(unsortedArray);
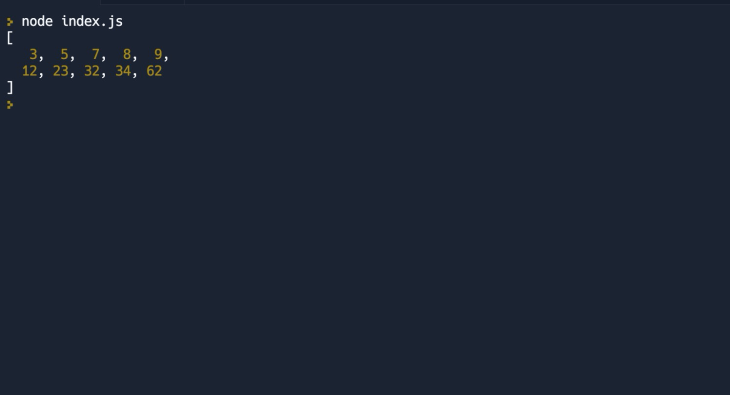
console.log(sortedArray);  // This will print the sorted array to the console.

The mergeSort function checks if the input array arr has one or fewer elements before starting the sorting operation. If not, it calculates the middle of the array and then divides it into two halves — left and right — before recursively sorting each half with the same mergeSort function.

On sorting the halves, the merge function merges them into one array after comparing elements from each array and appending them to the end of the result, ensuring a complete, sorted array.

Here’s the result of calling the function on an array with elements:

Merge sort has consistent O(n log n) time complexity in all cases, making it efficient for both small and large datasets. It’s also a stable sorting technique that preserves the order of equal elements.

Merge sort is commonly used in external sorting algorithms for large data sets that do not fit entirely in memory. It’s also used as a standard sorting algorithm due to its predictable performance.

Other relevant sorting algorithms

Many other sorting algorithms exist, including heapsort, bubble sort, and more. Here’s a brief introduction to some of them:

• Heapsort: Heapsort is an efficient and in-place comparison-based sorting algorithm. It’s often used when finding a dataset’s most minor or most significant elements
• Bubble sort: Bubble sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. It has limited practical use due to its O(n^2) time complexity, but it can be helpful for small datasets

Each sorting algorithm has strengths and weaknesses, making them suitable for specific scenarios. The sorting algorithm choice depends on data size, desired time complexity, and specific use case requirements.

Sorting algorithms in frontend vs. backend systems

Sorting algorithms have their place in both frontend and backend systems. Understanding the distinctions between frontend and backend sorting is essential for creating well-rounded applications.

Sorting in frontend systems

Sorting on the front end is a common operation, especially when dealing with datasets you must display to users in a specific order. The primary functions of sorting in frontend applications include:

• Improving UX: Frontend sorting significantly enhances UX by allowing users to interact and view data more effectively. It empowers users to customize how they perceive and access information, making applications more user-centric
• Displaying data interactively in UI components: Frontend sorting is commonly used in sorting tables, lists, or any UI components that present data to users. For instance, ecommerce websites often employ frontend sorting to enable users to sort product listings by price, popularity, or other criteria
• Updating data visualization tools in real-time: Frontend sorting enables real-time updates for data visualization tools and components based on user interaction. This dynamic behavior makes the UI more responsive, engaging, and satisfying to use

More often than not, JavaScript is the preferred way to implement frontend sorting, as it allows for real-time sorting without needing page reloads.

The efficiency of traditional sorting algorithms can vary based on the type and quantity of data you need to sort. In frontend apps, the time it takes to sort data can directly impact rendering times, overall application responsiveness, and user experience.

For example, let’s see what happens when using the bubbleSort function on a list with thousands of items to be rendered in a React component:

function bubbleSort(arr) {
    let n = arr.length;
    for (let i = 0; i < n-1; i++)
        for (let j = 0; j < n-i-1; j++)
            if (arr[j] > arr[j+1]) {
                let temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
    return arr;
}

function RenderList(props) {
    let sortedList = bubbleSort(props.data);
    return (
        <ul>
            {sortedList.map(item => <li key={item.id}>{item.value}</li>)}
        </ul>
    );
}

After re-rendering components, the program re-sorts the data, which may lead to a noticeable lag for larger datasets.

With real-time data visualization, data often comes in rapidly and needs to be incorporated into the visual representation just as quickly. Efficient sorting is crucial here, as slow sorting can introduce noticeable lag.

For instance, if you’re visualizing stock prices in real-time and new data comes in every second, you’d need to efficiently insert the new data point into the existing sorted dataset without re-sorting the entire dataset.

While the performance of sorting algorithms may not differ across frameworks, the way different frameworks detect data-changing models and trigger re-renders can vary.

For instance, React uses a virtual DOM to limit the number of actual DOM mutations. However, it can still be a bottleneck if the dataset changes frequently or the sorting operation is expensive.

Vue, on the other hand, uses a reactive data model. This means that sorting operations that change the dataset immediately trigger a re-render of the affected component.

Meanwhile, Angular uses change detection to determine when views should be updated. The strategy chosen — Default or OnPush — may influence how sorting operations impact rendering performance.

Sorting in backend systems

In backend systems, sorting is crucial for data processing, analytics, and server-side storage. Sorting impacts the order of result presentation to users. Some of its critical applications are:

• Data processing: Backend sorting ensures efficient data organization. This reduces the computational burden on the front end and enhances overall system performance
• Performance optimization: Backend sorting plays a significant role in optimizing the performance of database operations and data retrieval. You can use sorting algorithms to execute database queries more efficiently, resulting in faster response times
• Data storage: Database engines and languages often store data in a sorted order to facilitate quick searches and queries. Backend sorting is essential for maintaining this order and ensuring efficient data retrieval

Most of the sorting operations on your backend will be on your database. You’d typically implement sorting in your backend system with your preferred server-side programming language, such as Go, JavaScript, Python, or C++.

Data sorting looks slightly different for SQL databases and NoSQL databases. Here are some critical aspects of sorting in SQL databases:

• ORDER BY clause: SQL databases provide the ORDER BY clause, which allows you to sort query results based on one or more columns. You can sort based on ascending or descending order
• Indexing: Indexing can make sorting more efficient by allowing the database engine to locate data quickly and retrieve sorted data, thereby reducing the need for time-consuming scans
• Complex sorting: Most SQL databases support complex sorting criteria, including sorting by multiple columns or applying custom sorting rules using expressions or user-defined functions. This flexibility is essential for tailoring query results to specific application requirements

On the other hand, sorting in NoSQL databases involves the following:

• Dynamic schema: NoSQL databases often have a dynamic schema, allowing you to store different data types in the same collection or table. Sorting in this context can be more challenging since the structure of documents or records may vary
• Aggregation frameworks: Many NoSQL databases offer powerful aggregation frameworks that allow you to perform complex sorting, grouping, and transformation operations on data. This may be advantageous for apps requiring real-time analytics or extensive data processing
• Secondary indexes: NoSQL databases rely on secondary indexes to enable sorting. You can create indexes on specific fields for efficient sorting

To optimize backend database queries with sorting, you must consider various factors, including the volume of data, query complexity, and the specific database management system you use.

You can use techniques like indexing, batch processing, pagination, asynchronous sorting, and caching for faster operations.

Factors to consider when choosing a sorting technique

As we already know, choosing the right sorting technique depends on several factors, including the data quantity, nature, stability requirements, and memory and space constraints. Let’s discuss some of these in more detail now.

Data size

A primary consideration when choosing a sorting algorithm is the size of the dataset. Different algorithms have varying performance characteristics that make them suitable for specific data sizes.

For small data sets, the choice of sorting algorithm may not significantly impact performance. Simple algorithms like insertion sort or selection sort can be efficient enough and easy to implement.

When dealing with medium-sized data sets, algorithms like merge sort, quicksort, or heap sort may be more efficient. These algorithms have better average and worst-case time complexity and can handle larger data sets without performance bottlenecks.

Considering time complexity and memory usage becomes crucial for large data sets. Quicksort and heap sort are often preferred due to their relatively low memory requirements and efficient average-case performance.

Nature of the data

The nature of the data you are sorting can significantly impact the choice of sorting algorithm. Different algorithms exhibit different behaviors with specific data characteristics.

If the data set contains numerous duplicate values, the efficiency of sorting algorithms may vary. Quicksort struggles in these situations, often resulting in uneven partitions. On the other hand, merge sort and heap sort are more adept at handling duplicates, preserving the relative order of identical elements.

However, suppose you’re handling partially sorted data. In that case, you can use algorithms like insertion sort to achieve a linear time complexity, since quicksort and heap sort might face their most challenging scenarios with sorted or reverse-sorted data.

Memory and space constraints

You can classify sorting algorithms into two categories based on memory usage: in- and out-of-place sorting.

In-place sorting algorithms like quicksort, bubble sort, and insertion sort require only constant memory for temporary variables, regardless of the data set size. These algorithms are suitable for limited memory.

On the other hand, out-of-place sorting algorithms require additional memory space proportional to the size of the data. Merge sort is a classic example of an out-of-place sorting algorithm. While they may use more memory, out-of-place algorithms are often more stable and can be more straightforward.

Choosing between in-place and out-of-place sorting depends on the available memory and your application’s specific requirements. If memory is not a concern, you can opt for an out-of-place algorithm that may offer better stability and ease of implementation.

Comparison table for sorting algorithms

Let’s quickly summarize what we’ve discussed so far in the comparison table below:

Algorithm	Memory usage	Best for…	Average case time complexity	Worst case time complexity	Space complexity	Most stable complexity
Insertion sort	In-place sorting; requires constant memory for temporary variables	Small data sets	Partially sorted data	Limited memory	O(n^2)	O(n^2)
Selection sort	In-place sorting; requires constant memory for temporary variables	Small data sets	–	O(n^2)	O(n^2)	O(1)
Merge sort	Out-of-place sorting; requires memory space proportional to data size	Medium-sized data sets	Handling duplicates	O(n log n)	O(n log n)	O(n)
Quicksort	In-place sorting; requires constant memory for temporary variables	Medium to large data sets	Handling duplicates	O(n log n)	O(n^2)	O(log n)
Heapsort	In-place sorting; requires constant memory for temporary variables	Medium to large data sets	–	O(n log n)	O(n log n)	O(1)
Bubble sort	In-place sorting; requires constant memory for temporary variables	–	–	O(n^2)	O(n^2)	O(1)
Radix sort	Out-of-place sorting; requires memory space proportional to data size	Large data sets	Integers	O(kn)	O(kn)	O(k)

You can use this table to help guide your decision regarding which sorting algorithm to implement in your next project.

Conclusion

This article discussed popular sorting algorithms and how to implement them with JavaScript. You also learned about the importance of and differences between implementing sorting in your frontend and backend applications.

Choosing the suitable sorting algorithm for a specific task depends on various factors, including the size of the dataset, the desired level of sorting efficiency, and the stability requirements of the algorithm. I hope this guide will be helpful as you determine which technique is best for your needs.