
A palindrome is a sequence of characters that reads the same backwards as forwards. This sequence of characters could be a word, phrase, number, etc. For example, the word rotor remains the same even when the characters are read backwards.

In this tutorial, we will write a simple function called isPalindrome(chars) that takes a sequence of characters as input and returns true if the sequence is a palindrome, and false if it isn’t.
We will implement the algorithm for this function in JavaScript using recursion, but it can also be implemented in any other language of your choosing.
The Replay is a weekly newsletter for dev and engineering leaders.
Delivered once a week, it's your curated guide to the most important conversations around frontend dev, emerging AI tools, and the state of modern software.
For a start, let’s assume the sequence of characters passed to the function is a string. The string may contain non-alphanumeric characters like spaces, underscores, etc. In such cases, the string needs to be cleaned up and normalized.
Therefore, for most algorithms, the logical first step will be to remove all non-alphanumeric characters from the string and convert the string to lowercase. This makes it possible for palindrome phrases that may contain spaces, for example, to also pass the check.
In JavaScript, we can use this regular expression (/[^a-z0-9]/i) to strip off non-alphanumeric characters from the string. Given a string string, here is how we can get its normalized form:
// remove non-alphanumeric characters and // change the string to lowercase string.replace(/[^a-z0-9]/i, '').toLowerCase()
There are a number of algorithms for checking whether a string is a palindrome, using built-in language methods and loops. Here are two of the most popular ones:
The simplest algorithm will be to compare the string with its reversed string. If they match, the string is a palindrome; otherwise, it is not. This implementation of this algorithm can be achieved using built-in JavaScript methods and utilities.
The algorithm is as follows:
true if they match and false otherwiseHere is the implementation of this algorithm:
function isPalindrome (str) {
// remove non-alphanumeric characters and
// change the string to lowercase
str = str.replace(/[^a-z0-9]/i, '').toLowerCase();
// compare the string to the reversed string (if not empty)
// `Array.from(str)` is ES6 syntax for creating array of string characters.
// The ES5 equivalent will be to use: `str.split('')`
return (str.length > 0) && Array.from(str).reverse().join('') === str;
}
Another very popular algorithm is to loop through the characters of the string starting from the first character up to the character at the midpoint, comparing each character with the character at the corresponding position from the end of the string.
The algorithm is as follows:
// Using Math.floor() Math.floor(string.length / 2) // Using Math.ceil() Math.ceil((string.length - 1) / 2) // Using Bitwise Sign-Propagating Right Shift (>>) string.length >> 1
false. If the loop reaches the end and the function hasn’t returned already, return trueHere is the implementation of this algorithm:
function isPalindrome (str) {
let len = 0;
// remove non-alphanumeric characters and
// change the string to lowercase
// and get the length of the string
str = str.replace(/[^a-z0-9]/i, '').toLowerCase();
len = str.length;
// calculate the string midpoint position and
// loop through the characters up to the midpoint
// comparing characters in corresponding positions
// from the start of the string and the end of the string
for (let i = 0, mid = len >> 1; i < mid; i++) {
if (str[i] !== str[len - i - 1]) return false;
}
// if execution reaches here, the character comparisons matched
// and the string (if not empty) must be a palindrome
return len > 0;
}
As you may already know, a good number of algorithms that can be implemented using a loop can also be implemented using some form of recursion. Let’s go through how we can re-implement the isPalindrome() function using recursion.
For our recursive solution, we can identify two terminal conditions that can cause the recursion to stop and return a result immediately:
<=1), for which we return true.false should be returned from the function.For a basic implementation of our recursive solution, the following steps are executed in order when the function is invoked with a given string:
Here is what the implementation described above looks like:
function isPalindrome (str) {
// remove non-alphanumeric characters and
// change the string to lowercase
str = str.replace(/[^a-z0-9]/i, '').toLowerCase();
// and get the length of the string
const len = str.length;
if (len <= 1) return true;
if (str[0] !== str[len - 1]) return false;
// proper tail call optimized recursion
return isPalindrome(str.slice(1, -1));
}
Our function works as expected, but it still has a few issues we should fix, and we can make some optimizations to further improve it:
true instead of falseWe can use an immediately invoked function expression (IIFE) to return an isPalindrome() function that implements workarounds for these issues.
Inside the returned isPalindrome() function, we will normalize the string only once and also return false immediately if the normalized string is empty. Otherwise, we will pass the normalized string to an internal recursive _isPalindrome() function that is only accessible within the scope of the IIFE via closure.
Enough of the technical jargon — here is the modified version of the previous isPalindrome() function with some optimizations:
const isPalindrome = (() => {
/**
* This function is returned immediately
* from the invocation of the outer arrow function
* and is assigned to the `isPalindrome` identifier.
*/
return function isPalindrome (str) {
// remove non-alphanumeric characters and
// change the string to lowercase
str = str.replace(/[^a-z0-9]/i, '').toLowerCase();
// call the recursive _isPalindrome function with string (if not empty)
// and return the result
return (str.length > 0) && _isPalindrome(str);
};
/**
* Internal recursive `_isPalindrome()` function
* optimized for recursion with proper tail call.
*
* A single reference to this function is created and stored
* after the immediate invocation of the outer arrow function,
* not accessible outside the scope of the outer arrow function,
* but accessible to `isPalindrome()` via closure.
*/
function _isPalindrome (str) {
const len = str.length;
if (len <= 1) return true;
if (str[0] !== str[len - 1]) return false;
// proper tail call
return _isPalindrome(str.slice(1, -1));
}
})();
So far, our recursive solution works fine and is already optimized for tail call elimination (Proper Tail Calls). Tail call optimization is a new addition to JavaScript functions in the ES6 specification, meant to eliminate the issue of the JavaScript engine creating too many stack frames for recursive functions.
As far as support goes, tail call elimination is lagging behind across the major browsers. At the time of writing, Safari is the only browser that offers reasonable support for it.
However, if we are paranoid and want an optimized version of our recursive function that will work across all browsers, we can wrap our function in a trampoline. A trampoline can be used to wrap a function such that it runs as though it was tail call-optimized.
The trampoline is a higher-order function — it accepts the recursive function as its argument and returns another function. The returned function uses a while loop to repeatedly invoke the function returned from the last function invocation (starting with the recursive function) until a function is no longer returned.
Here is a typical trampoline:
const trampoline = fn => (...args) => {
let result = fn(...args);
while (typeof result === 'function') {
result = result();
}
return result;
}
For the trampoline to work with our recursive function, we will have to return a function from our recursive function. So instead of this:
{
/* other code here */
return _isPalindrome(str.slice(1, -1));
}
We will have this:
{
/* other code here */
// return a function that calls the recursive function
return () => _isPalindrome(str.slice(1, -1));
}
The following code snippet shows the new, optimized version of our recursive function that uses a trampoline:
const isPalindrome = (() => {
return function isPalindrome (str) {
str = str.replace(/[^a-z0-9]/i, '').toLowerCase();
// wrap the recursive _isPalindrome function with _trampoline()
return (str.length > 0) && _trampoline(_isPalindrome)(str);
};
// trampoline() — higher-order function
function _trampoline (fn) {
return function _trampolined (...args) {
let result = fn(...args);
while (typeof result === 'function') {
result = result();
}
return result;
}
}
function _isPalindrome (str) {
const len = str.length;
if (len <= 1) return true;
if (str[0] !== str[len - 1]) return false;
// return a function that calls the recursive function
return () => _isPalindrome(str.slice(1, -1));
}
})();
Practically speaking, it is very unlikely to run into stack overflow issues with isPalindrome() like you could with a typical recursive function like factorial(), for example.
Thus, the recursive solution we came up with for the isPalindrome() function in this tutorial may not seem to benefit much from the optimization techniques used. That’s not to discourage you or trivialize our efforts in any way, however, because the optimization techniques we highlighted here could be used to delay stack overflow for most recursive functions.
Thanks for making time to go through this tutorial. I am really glad that you made it to the end, and do hope it was worth your time.
Debugging code is always a tedious task. But the more you understand your errors, the easier it is to fix them.
LogRocket allows you to understand these errors in new and unique ways. Our frontend monitoring solution tracks user engagement with your JavaScript frontends to give you the ability to see exactly what the user did that led to an error.
LogRocket records console logs, page load times, stack traces, slow network requests/responses with headers + bodies, browser metadata, and custom logs. Understanding the impact of your JavaScript code will never be easier!

Discover what’s new in The Replay, LogRocket’s newsletter for dev and engineering leaders, in the March 11th issue.

Buying AI tools isn’t enough. Engineering teams need AI literacy programs to unlock real productivity gains and avoid uneven adoption.

If your AI app or agent works perfectly in development but falls apart in production, you’re not alone. In a […]
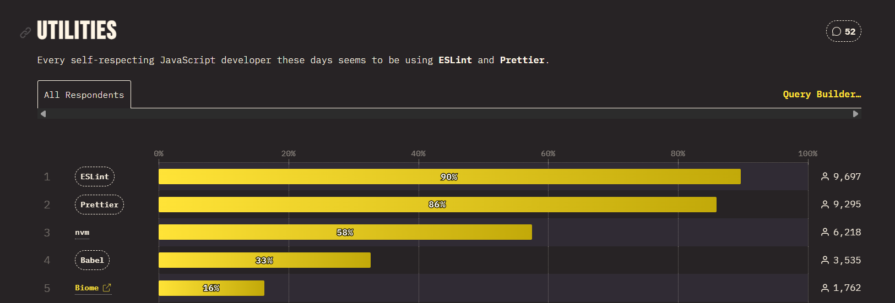
Compare ESLint and Oxlint, benchmark real speed gains, and learn when migrating to Oxlint makes sense for modern JavaScript teams.
Hey there, want to help make our blog better?
Join LogRocket’s Content Advisory Board. You’ll help inform the type of content we create and get access to exclusive meetups, social accreditation, and swag.
Sign up now