
If your AI app or agent works perfectly in development but falls apart in production, you’re not alone. In a […]
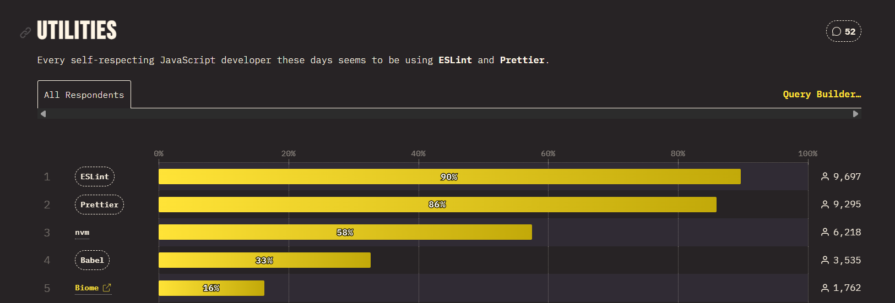
Compare ESLint and Oxlint, benchmark real speed gains, and learn when migrating to Oxlint makes sense for modern JavaScript teams.

Discover five practical ways to scale knowledge sharing across engineering teams and reduce onboarding time, bottlenecks, and lost context.

Discover what’s new in The Replay, LogRocket’s newsletter for dev and engineering leaders, in the March 4th issue.
Would you be interested in joining LogRocket's developer community?
Join LogRocket’s Content Advisory Board. You’ll help inform the type of content we create and get access to exclusive meetups, social accreditation, and swag.
Sign up now