How to represent large numbers in your Node.js app

It is difficult for computers to represent numbers with several significant digits accurately without loss of precision. Integers that exceed the maximum safe integer limit in JavaScript lose precision when you store them as ordinary integers.

In the JavaScript ecosystem, you can use BigInt to work with large integers. However, you can also use third-party packages with features similar to BigInt.

This article will be a complete guide to managing large numbers using BigInt and popular packages that offer similar features. We will also compare the third-party packages’ use cases, strengths, and weaknesses.

Jump ahead:

• How does JavaScript encode numbers?
  • The double-precision binary floating-point format
  • The minimum and maximum safe integers in JavaScript
  • Positive and negative infinity in JavaScript
• How to manage large integers in JavaScript using BigInt
• Packages for managing large numbers in JavaScript
  • Math.js
  • bignumber.js
  • JS Big Decimal
• Comparing packages for managing large numbers in JavaScript

How does JavaScript encode numbers?

The challenge of precision loss when representing large numbers is not unique to JavaScript. Internally, JavaScript uses the double-precision binary floating-point format to represent numbers.

The double-precision binary floating-point format

The double-precision binary floating-point format is defined by IEEE standard 754. It uses 64 bits to represent a signed floating point number. A number expressed in double-precision binary floating-point notation is comprised of three parts: the sign, mantissa, and exponent, as illustrated below:

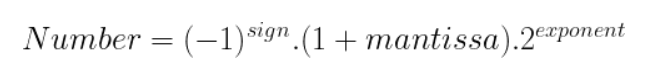
The double-precision binary floating-point format distributes the 64 bits among these three parts. It uses one bit to encode the sign, 11 bits for encoding the biased exponent, and 52 bits for the mantissa or significand.

The example below shows the internal double-precision binary floating-point number representation of the decimal number -1.7976931348623157e+308. I have used the • character to separate the encoding for the three parts.

The first bit encodes the sign. Because we are encoding a negative number, its value is one. If we were encoding a positive number, its value would be zero. The subsequent 11 bits encode the biased exponent, and the last 52 encode the mantissa:

1•11111111110•1111111111111111111111111111111111111111111111111111

Computers only understand binary. Therefore, JavaScript internally converts each number to a double-precision binary floating-point format, like in the exampleabove, before storing or performing mathematical operations.

Unfortunately, you cannot accurately and precisely represent some numbers in binary. Therefore, some numbers will lose precision when you convert them from decimal to binary and back to decimal.

Similarly, JavaScript uses a fixed number of bits for encoding the different parts of a double-precision binary floating-point number. Therefore, you’d use a third-party package or the built-in bigint type when dealing with large integers.

The minimum and maximum safe integers in JavaScript

Because the double-precision format limits the number of bits representing the mantissa to 53, there are limitations to the precision and accuracy of JavaScript integers with which you can work.

The maximum safe integer you can work with without losing precision is 2 ** 53 - 1. It is also a static data property of the Number constructor accessible using Number.MAX_SAFE_INTEGER:

console.log(2 ** 53 - 1 === Number.MAX_SAFE_INTEGER) // true

There is also a corresponding minimum safe integer whose value is -(2 ** 53 - 1). You can access its value using the Number.MIN_SAFE_INTEGER static property:

console.log(-(2 ** 53 - 1) === Number.MIN_SAFE_INTEGER) // true

Any mathematical operation you perform involving integers greater than the maximum safe integer or integers less than the minimum safe integer will lead to unexpected approximate results:

const maxSafeInteger = Number.MAX_SAFE_INTEGER;
const minSafeInteger = Number.MIN_SAFE_INTEGER;

console.log(maxSafeInteger + 1); // 9007199254740992
console.log(maxSafeInteger + 2); // 9007199254740992
console.log(maxSafeInteger + 1 === maxSafeInteger + 2); // true

console.log(minSafeInteger - 1); // -9007199254740992
console.log(minSafeInteger - 2); // -9007199254740992
console.log(minSafeInteger - 1 === minSafeInteger - 2); // true

Positive and negative infinity in JavaScript

Like the minimum and maximum safe integers above, JavaScript has a maximum numeric value it can represent internally. This value is 2 ** 2014 - 1. You can access it using the Number.MAX_VALUE data property.

JavaScript represents any numeric value exceeding Number.MAX_VALUE using Infinity and the corresponding negative equivalent using -Infinity, like in the examples below:

console.log(Number.MAX_VALUE * 2); // Infinity
console.log(Number.MAX_VALUE * 3); // Infinity
console.log(-Number.MAX_VALUE * 3); // -Infinity

Though Infinity is global in Node, you can access it using the Number.POSITIVE_INFINITY data property and -Infinity using the Number.NEGATIVE_INFINITY data property.

How to manage large integers in JavaScript using BigInt

As hinted in the introduction section, JavaScript uses the double-precision format to represent numbers internally. Because it uses 53 bits to encode the mantissa, the maximum safe integer you can work with in JavaScript is 2**53 - 1.

To safely work with integers greater than the maximum safe integer, you need the bigint primitive. It is the built-in functionality for manipulating large integers without losing precision.

You can create a bigint type by appending n to an integer or using the BigInt function. Because BigInt is not a constructor, invoke it without the new keyword, like in the examples below:

const number = 1n;
console.log(1n + 2n); // 3n

const maxSafeInt = BigInt(Number.MAX_SAFE_INTEGER);
console.log(maxSafeInt + 1n); // 9007199254740992n
console.log(maxSafeInt + 2n); // 9007199254740993n
console.log(maxSafeInt * maxSafeInt); // 81129638414606663681390495662081n

Unlike the usual number type, you can’t use the built-in Math methods with BigInt values. However, you can perform basic math operations such as addition, subtraction, and exponentiation with bigint types:

console.log(2n + 3n) // 5n
console.log(2n - 3n)  // -1n
console.log(2n ** 3n) // 8n
console.log(4n % 3n)  // 1n
console.log(BigInt(3) - 4n) // -1n

As you can only perform basic math operations with bigint types, you may need to use a third-party package for some use cases when dealing with large numbers in JavaScript.

Packages for managing large numbers in JavaScript

In addition to the built-in bigint type, there are several third-party packages to work with large numbers in JavaScript. Some of these packages come with solutions that BigInt may not offer.

However, like any third-party package, there are downsides to using them. They come with extra bundle size, maintenance, security, and licensing issues.

Managing large numbers using Math.js

Math.js is a free, open source, and feature-packed math library. It is also isomorphic. Therefore, you can use it both in the browser and the Node runtime environment.

Though it is a feature-packed library, in this article, we will use Math.js for managing large numbers in the Node runtime environment. Depending on your package manager, install it from the npm package registry like this:

# npm 
npm i mathjs

# yarn
yarn add mathjs

#pnpm
pnpm add mathjs

After installing Math.js, you can load and use it with the default configuration, like in the example below:

const { add, subtract, evaluate }= require('mathjs');

const sum = add(2, 3);
const difference = subtract(2, 3);
const anotherSum = evaluate('2 + 3');

console.log(sum); // 5
console.log(difference}); // -1
console.log(anotherSum}); // 5

Instead of using the Math.js built-in functions with the default configuration, you can instead create an instance of Math.js with a custom configuration:

const { create, all } = require("mathjs");

const config = {};
const math = create(all, config);

console.log(math.add(2, 3)); // 5
console.log(math.pow(2, 3)); // 8
console.log(math.divide(4, 2)); // 2
console.log(math.multiply(2, 3)); // 6

Math.js has the BigNumber datatype specifically for working with large numbers.

In one of the sections above, we highlighted that when working with the built-in number type, JavaScript represents numbers exceeding the maximum representable numeric value using Infinity.

With Math.js, you can represent numbers exceeding the maximum representable number and perform mathematical operations on them. However, be aware that performing mathematical operations on BigNumber types is slower than on ordinary number types:

const { create, all } = require("mathjs");

const config = {};
const math = create(all, config);

const maxValue = math.bignumber(Number.MAX_VALUE);
console.log(math.add(maxValue, maxValue)); // 3.5953862697246314e+308

const maxSafeInt = math.bignumber(Number.MAX_SAFE_INTEGER);

console.log(math.square(maxSafeInt)); // 8.1129638414606663681390495662081e+31
console.log(math.add(maxSafeInt, maxSafeInt)); // 18014398509481982
console.log(math.subtract(maxSafeInt, maxSafeInt)); // 0
console.log(math.multiply(maxSafeInt, math.bignumber(2))); // 18014398509481982
console.log(math.divide(maxSafeInt, math.bignumber(2))); // 4503599627370495.5

console.log(math.log10(maxSafeInt)); // 15.95458977019100329811178809273377220616031325194798178472905735
console.log(math.pow(maxSafeInt, math.bignumber(2))); // 8.1129638414606663681390495662081e+31

The default precision for the BigNumber type is 64 digits. However, you can use the config object to configure Math.js to use a different precision level.

Managing large numbers using bignumber.js

bignumber.js is another JavaScript library for managing arbitrary-precision decimal and non-decimal arithmetic. It is a free, open source, MIT-licensed library for working with large numbers.

It runs in the browser, Node, and Deno. To start using bignumber.js, install it from the npm package registry:

# npm 
npm i bignumber.js

# yarn
yarn add bignumber.js

#pnpm
pnpm add bignumber.js

After installation, import and create an instance of the BigNumber constructor, which takes a number, string, or BigNumber type as an argument and returns an object.

In the example below, I use the commonjs syntax to import bignumber.js. It also supports ES syntax. If you intend to use bignumber.js in the browser environment without a JavaScript bundler, you can also access it via a CDN:

const BigNumber = require("bignumber.js");

const distanceOfTheSun = new BigNumber('1.49597870700e11'); // in metres
console.log(distanceOfTheSun) // BigNumber { s: 1, e: 11, c: [ 149597870700 ] }
console.log(distanceOfTheSun.valueOf()) // 149597870700

When using the built-in number type, JavaScript will represent any numeric value greater than Number.MAX_VALUE as Infinity. However, with bignumber.js, you can work with any value greater than the Number.MAX_VALUE.

In the example below, I am creating an instance of BigNumber by passing Number.MAX_VALUE as a string and computing its square. If you were to do the same using the built-in JavaScript number primitive, you would get Infinity:

const BigNumber = require("bignumber.js");

console.log(Number.MAX_VALUE); // 1.7976931348623157e+308
console.log(Number.MAX_VALUE ** 2) // Infinity

const maxValue = new BigNumber(Number.MAX_VALUE.toString());
const square = maxValue.exponentiatedBy("2");

console.log(square.valueOf()); // 3.23170060713109998320439596646649e+616

const squareRoot = square.squareRoot();
console.log(squareRoot.valueOf()); // 1.7976931348623157e+308
console.log(squareRoot.isEqualTo(maxValue)); // true

However, when working with such large numbers that are not representable in JavaScript, use either the toString or valueOf method to access the result of your computation as a string.

The toNumber method will coerce the result of your computation to a JavaScript number primitive. You will still encounter the same JavaScript big number problem highlighted above. Your answer will lose precision, or JavaScript will represent it as Infinity.

Though our goal in this article is to use the bignumber.js package to work with large numbers, bignumber.js also works with corresponding small numbers. It has several built-in methods that I haven’t highlighted here. Check out the documentation to learn the other built-in functions.

Managing large numbers using JS Big Decimal

JS Big Decimal is another JavaScript library you can use to work with large numbers. Unlike its counterparts above, JS Big Decimal has a small bundle size and comes with a limited set of features. You can use it to manage both large and small decimal numbers.

Depending on your package manager, use one of the commands below to install JS Big Decimal from the npm package registry:

# npm 
npm i js-big-decimal

# yarn
yarn add js-big-decimal

#pnpm
pnpm add js-big-decimal

Like the other two packages, import the BigDecimal constructor and create an instance like the example below. The BigDecimal constructor takes a number or a string as an argument and returns a BigDecimal object.

You can then use the getValue method to access the value of the number as a string. Alternatively, use getPrettyValue if you want to format the output:

const BigDecimal = require("js-big-decimal");

const value = new BigDecimal('23');
console.log(value.add(new BigDecimal(2)).getValue())

JS Big Decimal has functions for performing basic mathematical operations such as addition, subtraction, multiplication, and division. The code below illustrates how to use them to work with large numbers:

const BigDecimal = require("js-big-decimal");

const maxSafeInt = new BigDecimal(Number.MAX_SAFE_INTEGER.toString());
const divisor = new BigDecimal("2");

console.log(maxSafeInt.getPrettyValue()); // 9,007,199,254,740,991

const sum = maxSafeInt.add(maxSafeInt);
const quotient = maxSafeInt.divide(divisor);
const diff = maxSafeInt.subtract(quotient);
const product = quotient.multiply(divisor);

console.log(sum.getValue()); // 18014398509481982
console.log(quotient.getPrettyValue()); // 4,503,599,627,370,495.50000000
console.log(diff.getPrettyValue()); // 4,503,599,627,370,495.50000000
console.log(product.getPrettyValue()); // 9,007,199,254,740,991

Comparing packages for managing large numbers in JavaScript

Not all packages are created equal. Each third-party package has use cases, strengths, and weaknesses. Let’s compare the third-party packages above by highlighting their strengths and weaknesses and exploring metrics such as GitHub stars and issues, bundle size, and npm downloads.

It is worth noting that metrics such as GitHub stars are similar to social media likes. You may use it as a proxy indicator for the popularity of a package. However, it doesn’t tell you much about the quality.

Similarly, the npm download statistics are far from precise. According to npm, the download count is the number of served HTTP 200 responses that were tarball files. Therefore, the download count includes automated downloads by build servers, mirrors, and bots. Though the npm download count isn’t an accurate measure of the active users of a package, you can use it to make comparisons across packages.

	Math.js	bignumber.js	JS Big Decimal
Gzipped bundle size	187.93KB	8.09KB	3.88KB
Dependencies	9	0	0
GitHub stars	13.1k	6k	96
Active maintenance	Yes	Yes	Yes
Documentation	Good	Good	Good
License	Apache-2.0	MIT	MIT
npm weekly downloads	502,656	7,114,325	25,204
Pricing	Free	Free	Free
Open GitHub issues	157	14	6
Closed GitHub issues	1397	240	27

All the above third-party packages are free, open source libraries with permissive licenses. Among the three, Math.js is a feature-packed general math library, while the other two were created for managing large numbers.

Therefore, Math.js has the largest Gzipped bundle size. However, it is tree-shakable if you are using a bundler like webpack. Both Math.js and bignumber.js come with several features for managing large numbers and performing mathematical operations on them.

On the other hand, JS Big Decimal has the smallest bundle size. However, it also has the least number of features. It is only capable of performing basic mathematical operations.

Conclusion

JavaScript internally uses the 64 bit double-precision binary floating-point format to represent numbers. It allocates one bit to represent the sign, 11 bits for the exponent, and 53 bits to represent the mantissa.

JavaScript allocates fixed bits for representing the different parts of a double-precision floating point number. Therefore, it approximates integers outside the safe integer range. Similarly, it represents numeric values greater than Number.MAX_VALUE using Infinity and their corresponding negative values using -Infinity.

Though the built-in BigInt is useful for working with integers greater than the maximum safe integer or less than the minimum safe integer, it is lacking because you can only perform basic mathematical operations such as addition, subtraction, multiplication, and exponentiation. You can’t use it with methods of the built-in Math object; doing so will throw an error.

To work with large numbers in JavaScript without encountering the above limitations, you need third-party packages such as Math.js, bignumber.js, and JS Big Decimal. Though most third-party packages have limitations, as highlighted above, they have features that make working with large numbers a breeze.